Harnessing the Power of ClickHouse® Arrays – Part 3

In the second article on ClickHouse arrays, we explored how ClickHouse arrays are tightly coupled with GROUP BY expressions. This integration allows users to solve problems like enumerating sequences of events or performing funnel analysis.
This final article completes our tour of array capabilities. We’ll survey functions for array map and reduce operations, demonstrating behavior and commenting on performance. This is an opportunity to dig further into lambdas, which are critical for using arrays effectively. We will wrap things up by showing how to use arrays to perform linear interpolation and fill in missing values. If you can handle that example you are a ClickHouse array guru!
More Higher Order Functions: arrayMap() and arrayReduce
Higher order functions take other functions as arguments. We have already seen examples of this pattern in the previous article starting with the arraySort() function, which takes a lambda function to choose sort keys. We will expand on this pattern to demonstrate functions related to map and reduce operations, which are important functional programming tricks.
Let’s start with map operations. ClickHouse offers the arrayMap() function, which transforms array elements using a lambda expression. Here is a simple example to truncate strings.
WITH ['tiny', 'longer', 'longest'] AS array SELECT arrayMap(v -> substr(v, 1, 4), array) AS map ┌─map────────────────────┐ │ ['tiny','long','long'] │ └────────────────────────┘
As we showed in the previous article, array functions commonly allow multiple array arguments and arrayMap() is no exception. Here’s a more complex map function that truncates arrays using values from the second array function.
WITH ['tiny', 'longer', 'longest'] AS array, [2, 4, 6] AS length SELECT arrayMap((v, l) -> substr(v, 1, l), array, length) AS map ┌─map────────────────────┐ │ ['ti','long','longes'] │ └────────────────────────┘
We can also call on the arrayReduce() function to compute aggregates on arrays. arrayReduce() takes the name of an aggregate function as the first argument. (Unfortunately, it’s not possible to use lambda expressions to perform custom aggregations.) The following sample illustrates behavior.
WITH ['tiny', 'longer', 'longest'] AS array
SELECT
arrayMap(v -> length(v), array) AS map,
arrayReduce('sum', map) AS sum,
arrayReduce('avg', map) AS avg,
arrayReduce('count', map) AS count
┌─map─────┬─sum─┬────────────────€avg─┬─count─┐
│ [4,6,7] │ 17 │ 5.666666666666667 │ 3 │
└────────┴─────┴───────────────────┴────────┘The arrayReduce() function is quite efficient compared to alternatives. For instance, you can sum up array values using the arraySum() function, as shown in the next query.
SELECT arraySum(range(1, 100000000)) ┌─arraySum(range(1, 100000000))─┐ │ 4999999950000000 │ └───────────────────────────────┘ 1 rows in set. Elapsed: 0.963 sec.
Let’s try the same thing with arrayReduce().
SELECT arrayReduce('sum', range(1, 100000000))
┌─arrayReduce('sum', range(1, 100000000))─┐
│ 4999999950000000 │
└─────────────────────────────────────────┘
1 rows in set. Elapsed: 0.289 sec. arrayReduce() is vectorized and hence faster than arraySum(). As we have seen before, it is important to test performance when alternative approaches are available. This particular tradeoff is difficult to deduce from the ClickHouse logs–you just have to try it.
Finally, there are creative ways to combine arrayMap() and arrayReduce() operations. Here is an example that uses arrays to compute a weighted average. The trick is to use a lambda to map values from multiple arrays to a single vector of values. The first two results are provided for comparison.
WITH
[1, 2, 3, 4, 5] AS values,
[0.2, 0.2, 0.2, 0.2, 0.2] AS std,
[0.2, 0.2, 0.3, 0.25, 0.05] AS weights
SELECT
arrayReduce('avg', values) AS mean,
arrayReduce('sum', arrayMap((v, w) -> (v * w), values, std)) AS mean2,
arrayReduce('sum', arrayMap((v, w) -> (v * w), values, weights)) AS weighted
┌─mean─┬─mean2─┬─weighted─┐
│ 3 │ 3 │ 2.75 │
└─────┴───────┴───────────┘Note that the avgWeighted() function provides an alternative for weighted averages. It does not require the lambda. Once again, ClickHouse has multiple ways to solve a problem. When in doubt, try them out and pick the one that works best.
The Grand Finale: Using arrays to perform linear interpolation
We promised an advanced example of arrays, so here it is: linear interpolation. This is a problem that is difficult to solve in conventional SQL. Let’s start by imagining a test table with sensor data. Here is the CREATE TABLE statement.
CREATE TABLE readings ( datetime DateTime, sensor UInt32, temp Float32 ) ENGINE=MergeTree PARTITION BY toYYYYMM(datetime) ORDER BY (sensor, datetime)
Let’s insert 24 hours worth of readings.
INSERT INTO readings (datetime, sensor, temp)
WITH
toDateTime(toDate('2020-01-01')) as start_time
SELECT
start_time + number*60*60 as datetime,
23,
if (rand32() % 5 = 0, 0, 50.0 + sin(((number % 24)/24. * 2 * 3.14159) - 3.14159) * 15.0) as temp
FROM system.numbers_mt
LIMIT 24It may not be obvious what the SQL code is doing, so we will graph the data using the handy ClickHouse bar() function. The readings are a sine function with missing values.
SELECT datetime, temp, bar(temp, 30., 65., 50) FROM readings ┌─────────────€datetime─┬───────€temp─┬─bar(temp, 30., 65., 50)────────────────────────────┐ │ 2020-01-01 00:00:00 │ 49.99996 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ │ │ 2020-01-01 01:00:00 │ 46.11768 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 02:00:00 │ 42.49997 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ │ │ 2020-01-01 03:00:00 │ 39.393375 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 04:00:00 │ 37.009605 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ │ │ 2020-01-01 05:00:00 │ 35.51111 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ │ │ 2020-01-01 06:00:00 │ 35 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ │ │ 2020-01-01 07:00:00 │ 0 │ │ │ 2020-01-01 08:00:00 │ 37.009624 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ │ │ 2020-01-01 09:00:00 │ 39.393406 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 10:00:00 │ 42.500008 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ │ │ 2020-01-01 11:00:00 │ 46.117718 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 12:00:00 │ 50 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 13:00:00 │ 53.882282 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 14:00:00 │ 57.499992 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 15:00:00 │ 60.606594 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 16:00:00 │ 0 │ │ │ 2020-01-01 17:00:00 │ 64.488884 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 18:00:00 │ 65 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ │ │ 2020-01-01 19:00:00 │ 64.48889 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 20:00:00 │ 62.990395 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 21:00:00 │ 60.606625 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 22:00:00 │ 57.50003 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 23:00:00 │ 53.88232 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │
Our assignment is to fill in missing readings. One common approach is to use linear interpolation–just take the average of the previous and succeeding values. This is a job for arrays, but how exactly do we proceed?
First, let’s recall a bit of high school math regarding how interpolation works. Here’s the formula to interpolate a Y value for X given upper and lower values on either side.
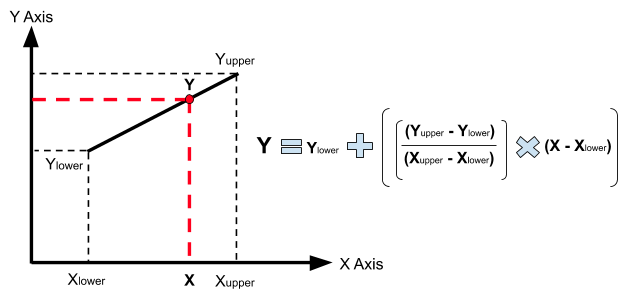
We commence by finding X and Y bounds on either side of missing values. There are many ways to attack this problem. We will choose the handy arrayFill() and arrayReverseFill() functions. These functions back fill and forward fill array positions using a lambda to decide whether to replace the current cell with a preceding or succeeding value. In this case we’re looking for non-zero values. Here’s an example of filling in lower and upper temperature values.
WITH [1.1, 3.3, 0., 0., 9.9] AS temp_arr SELECT temp_arr, arrayFill(x -> (x > 0), temp_arr) AS lower, arrayReverseFill(x -> (x > 0), temp_arr) AS upper FORMAT Vertical Row 1: ───────€ temp_arr: [1.1,3.3,0,0,9.9] lower: [1.1,3.3,3.3,3.3,9.9] upper: [1.1,3.3,9.9,9.9,9.9]
Temperature is our Y value. We also need the lower and upper datetime values, which is the X. We can pair X and Y values using the arrayZip() function. Adding this to the previous examples we get filled-in lower and upper values as tuples. Note that in the lambda we can refer to the tuple values as x.1 (the first value) and x.2 (the second value).
WITH
[toDateTime('2020-01-01 00:00:00'),
toDateTime('2020-01-01 01:00:00'),
toDateTime('2020-01-01 02:00:00'),
toDateTime('2020-01-01 03:00:00'),
toDateTime('2020-01-01 04:00:00')] AS dt_arr,
[1.1, 3.3, 0., 0., 9.9] AS temp_arr
SELECT
dt_arr,
temp_arr,
arrayFill(x -> ((x.1) > 0), arrayZip(temp_arr, dt_arr)) AS lower,
arrayReverseFill(x -> ((x.1) > 0), arrayZip(temp_arr, dt_arr)) AS upper
FORMAT Vertical
Row 1:
───────€
dt_arr: ['2020-01-01 00:00:00','2020-01-01 01:00:00','2020-01-01 02:00:00','2020-01-01 03:00:00','2020-01-01 04:00:00']
temp_arr: [1.1,3.3,0,0,9.9]
lower: [(1.1,'2020-01-01 00:00:00'),(3.3,'2020-01-01 01:00:00'),(3.3,'2020-01-01 01:00:00'),(3.3,'2020-01-01 01:00:00'),(9.9,'2020-01-01 04:00:00')]
upper: [(1.1,'2020-01-01 00:00:00'),(3.3,'2020-01-01 01:00:00'),(9.9,'2020-01-01 04:00:00'),(9.9,'2020-01-01 04:00:00'),(9.9,'2020-01-01 04:00:00')]We now add arrayMap() and perform linear interpolation of values. The arrayMap() call depends on a complex lambda that either takes the current temperature value if available or the interpolated value if not. In the latter case we compute the temperature using our formula for linear interpolation. Due to lambda syntax for tuples, the Y values are “1” and X values are “2” in the ClickHouse code. With this in mind, you should be able to read the interpolation formula terms without too much effort.
WITH
[toDateTime('2020-01-01 00:00:00'),
toDateTime('2020-01-01 01:00:00'),
toDateTime('2020-01-01 02:00:00'),
toDateTime('2020-01-01 03:00:00'),
toDateTime('2020-01-01 04:00:00')] AS dt_arr,
[1.1,3.3,0.0,0.0,9.9] AS temp_arr
SELECT dt_arr, temp_arr,
arrayFill(x -> ((x.1) > 0), arrayZip(temp_arr, dt_arr)) as lower,
arrayReverseFill(x -> ((x.1) > 0), arrayZip(temp_arr, dt_arr)) as upper,
arrayMap((l, u, t, dt) ->
if(t > 0,
t,
l.1 + ((u.1 - l.1) / (u.2 - l.2) * (dt - l.2))
), lower, upper, temp_arr, dt_arr) AS temp_arr_corrected
FORMAT Vertical
Row 1:
───────€
...
temp_arr: [1.1,3.3,0,0,9.9]
...
temp_arr_corrected: [1.1,3.3,5.5,7.7,9.9]The input values were chosen to make it easy to see that our results are correct. We have all the array logic to do interpolation on missing values. It is now a short step to build a complete query that solves our original problem.
SELECT datetime, temp_corrected, bar(temp_corrected, 30., 65., 50) FROM ( SELECT toDate(datetime) AS day, groupArray(datetime) AS dt_arr, groupArray(temp) AS temp_arr, arrayFill(x -> ((x.1) > 0), arrayZip(temp_arr, dt_arr)) as lower, arrayReverseFill(x -> ((x.1) > 0), arrayZip(temp_arr, dt_arr)) as upper, arrayMap((l, u, t, dt) -> if(t > 0, t, l.1 + ((u.1 - l.1) / (u.2 - l.2) * (dt - l.2)) ), lower, upper, temp_arr, dt_arr) AS temp_arr_corrected FROM readings GROUP BY day ORDER BY day ASC ) ARRAY JOIN dt_arr AS datetime, temp_arr_corrected AS temp_corrected ┌─────────────€datetime─┬──────€temp_corrected─┬─bar(temp_corrected, 30., 65., 50)──────────────────┐ │ 2020-01-01 00:00:00 │ 49.999961853027344 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ │ │ 2020-01-01 01:00:00 │ 46.117679595947266 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 02:00:00 │ 42.499969482421875 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ │ │ 2020-01-01 03:00:00 │ 39.393375396728516 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 04:00:00 │ 37.009605407714844 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ │ │ 2020-01-01 05:00:00 │ 35.5111083984375 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ │ │ 2020-01-01 06:00:00 │ 35 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ │ │ 2020-01-01 07:00:00 │ 36.004812240600586 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 08:00:00 │ 37.00962448120117 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ │ │ 2020-01-01 09:00:00 │ 39.39340591430664 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 10:00:00 │ 42.50000762939453 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ │ │ 2020-01-01 11:00:00 │ 46.11771774291992 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 12:00:00 │ 50 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 13:00:00 │ 53.88228225708008 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 14:00:00 │ 57.49999237060547 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 15:00:00 │ 60.60659408569336 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 16:00:00 │ 62.547739028930664 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 17:00:00 │ 64.48888397216797 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 18:00:00 │ 65 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ │ │ 2020-01-01 19:00:00 │ 64.4888916015625 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 20:00:00 │ 62.990394592285156 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 21:00:00 │ 60.606624603271484 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ │ 2020-01-01 22:00:00 │ 57.500030517578125 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€Œ │ │ 2020-01-01 23:00:00 │ 53.882320404052734 │ €ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€ˆ€‹ │ └────────────────────┴────────────────────┴─────────────────────────────────────────────────────┘
It would be nice to say that the if() function saves us some interpolation effort, but actually that’s not the case. If() computes both branches and then uses one of them based on the condition. So we don’t actually save processing, at least in recent ClickHouse implementations. (This example is based on version 20.6.)
Epilog on Arrays and Lambdas
Array processing uses lambdas extensively, and the resulting queries can be real doozies if you are ambitious. It would be easier to read and maintain query code if we could store lambdas separately and refer to them in later queries.
It turns out that there is work on the ClickHouse roadmap to implement user-defined functions (UDFs). Completion is planned for Q2 2021. We will revisit array processing at that time to see if some of the lambdas in this series can be simplified. If so, it will open up even more opportunities to use arrays productively in applications.
Series Conclusion
Over the course of this series of blog articles we dug deeply into ClickHouse arrays and provided numerous illustrations of their power. There were many points but here are a few major takeaways.
- ClickHouse arrays can unroll into tables using ARRAY JOIN. Tabular format is easier for both humans as well as many SQL-based applications to consume. It also allows you to do computations on arrays, turn the intermediate results into a table, and use normal SQL from then on.
- ClickHouse arrays are tightly linked with GROUP BY results through the groupArray() function. You can convert grouped values into arrays to perform complex computations within the group, such as enumerating sequences of events. In this sense, arrays provide capabilities similar to window functions in other databases.
- ClickHouse offers a rich array of functions to process array data. Many of these are higher order functions that take lambda expressions as arguments. Lambdas are key to unlocking advanced array features.
It is not possible to cover every aspect of array behavior in a short set of articles. We hope, however, that we provided sufficient background to use arrays to solve problems unique to your own applications. If you have questions about arrays or ClickHouse in general, don’t hesitate to contact us. We love working with ClickHouse and helping users apply its unique capabilities successfully.
Note: My thanks to Dmitry Titov and Christina Hodges for suggestions on the linear interpolation example.
ClickHouse® is a registered trademark of ClickHouse, Inc.; Altinity is not affiliated with or associated with ClickHouse, Inc.
