Learning to appreciate monotonic functions in ClickHouse®

If you love ClickHouse®, Altinity can simplify your experience with our fully managed service in your cloud (BYOC) or our cloud and 24/7 expert support. Learn more.
Introduction
ClickHouse has an amazing number of optimizations that enable it to fetch data quickly, often involving math concepts that don’t sound particularly interesting to most users. One such optimization involves monotonically increasing functions (say that five times fast). Deep under the hood of ClickHouse code, there are clever optimizations that use the mathematical concept of monotonicity to skip over unnecessary data. This article will define monotonicity as a math concept and give examples of monotonic functions in SQL. Then, we’ll look at why this matters in ClickHouse and how it could be improved.
Demos in this blog use an Altinity.Cloud server running on an AWS m5.large instance with ClickHouse version 24.4.3. For each of my algorithms, I give execution time as the average time of five trials. For some of my examples, I included pictures of graphs that I made in Desmos and bar graphs made using Bar Graph Maker.
A small example in ClickHouse
To show why you should care about monotonicity, here’s a small example. Below, I have two similar queries running over a table called ontime_ref on the Altinity demo server, which contains flight data from 1987 to 2020. In the first query, I count the number of flights taking place in the year 2015, while in the second example, I count the number of flights taking place in the 21st week of the year. First, I run the following command, which lasts for the whole clickhouse-client session:
SET min_bytes_to_use_direct_io = 1This command applies a setting which forces ClickHouse to go to storage instead of reading out of the OS buffer cache. It gives more consistent results based on the actual data that ClickHouse needs to read. Next, I run the three queries:
SELECT count()
FROM default.ontime_ref
WHERE toYear(FlightDate) = 2015toYear(): Average execution time: 0.076 seconds
SELECT count()
FROM default.ontime_ref
WHERE toWeek(FlightDate) = 21toWeek(): Average execution time = 0.2562 seconds
SELECT count()
FROM default.ontime_ref
WHERE toString(toYear((FlightDate)) = '2015'toString(): Average execution time = 0.5128 seconds
I was surprised that these three queries, which look so similar in form, in fact have very different execution times. What makes the second query 3x slower than the first, and the third query 2x slower than the second? To understand why this is the case, we first have to understand the power of monotonicity in mathematics and in ClickHouse. A hint is George Orwell’s observation in Animal Farm: “All animals are equal, but some animals are more equal than others.” In our case, both toYear() and toWeek() are monotonic, but one is “more monotonic” than the other; that is what creates the difference in execution time.
Defining monotonicity
A monotonically increasing function is one where increasing the inputs results in an equal or larger output. A simple example of a single-variable, monotonically increasing function in SQL is sqrt(), the square root function. As the variable x increases, as does the value of sqrt(x).
SELECT number AS x, sqrt(x) FROM numbers(11)
┌───x─┬────────────sqrt(x)─┐
│ 0 │ 0 │
│ 1 │ 1 │
│ 2 │ 1.4142135623730951 │
│ 3 │ 1.7320508075688772 │
│ 4 │ 2 │
│ 5 │ 2.23606797749979 │
│ 6 │ 2.449489742783178 │
│ 7 │ 2.6457513110645907 │
│ 8 │ 2.8284271247461903 │
│ 9 │ 3 │
│ 10 │ 3.1622776601683795 │
│ 11 │ 3.3166247903554 │
│ 12 │ 3.4641016151377544 │
│ 13 │ 3.605551275463989 │
│ 14 │ 3.7416573867739413 │
│ 15 │ 3.872983346207417 │
│ 16 │ 4 │
└─────┴────────────────────┘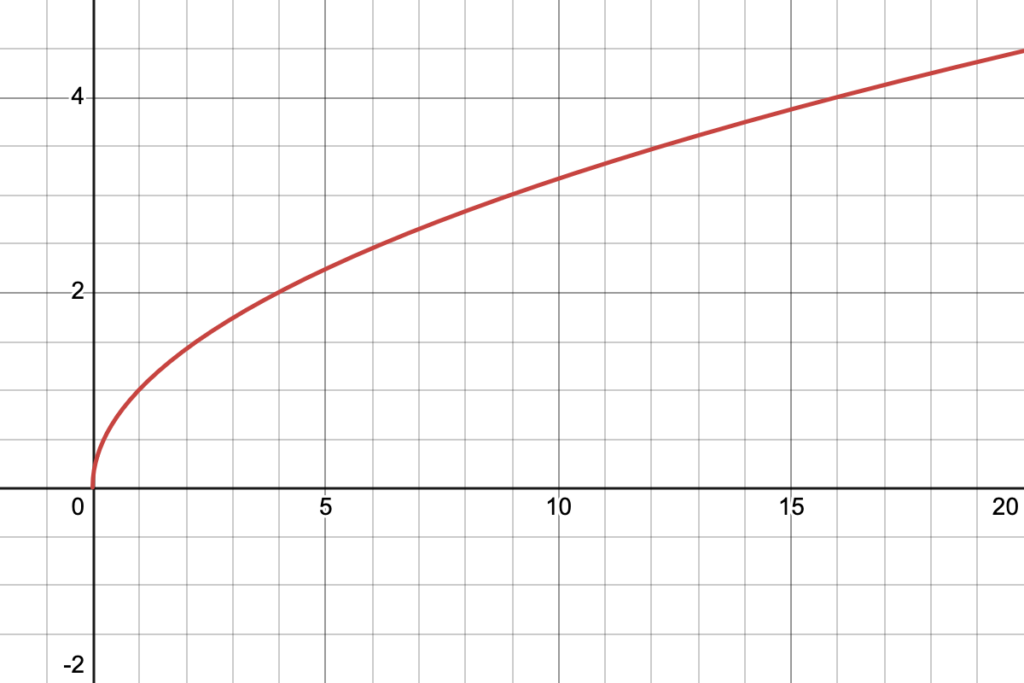
sqrt() is monotonically increasing because for all x, y ≥ 0, x ≤ y ⇒ sqrt(x) ≤ sqrt(y). sqrt() is a stronger case of monotonicity; since it is always increasing on its domain, we call this function strictly increasing. “Monotonically increasing” is the same as saying sqrt() is “non-decreasing” and that sqrt() “preserves the order of the inputs.” So if sqrt() takes the range [a, b] as inputs, then we know that all outputs will be in the range [sqrt(a), sqrt(b)].
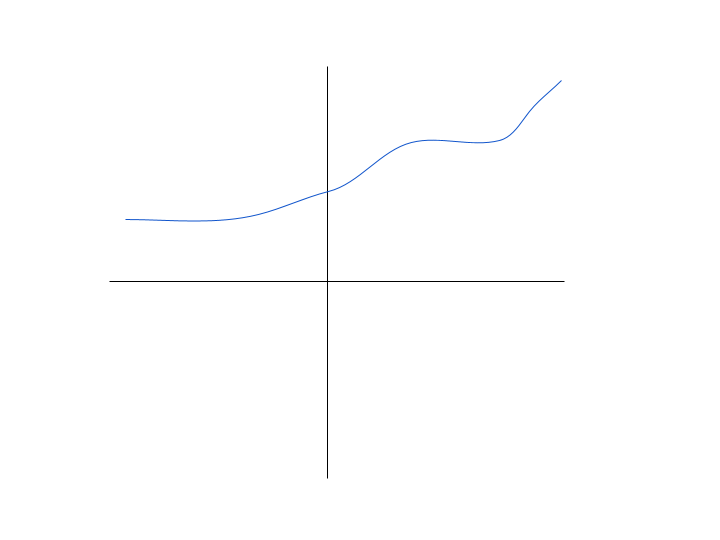
In general, a monotonically increasing function looks something like this:
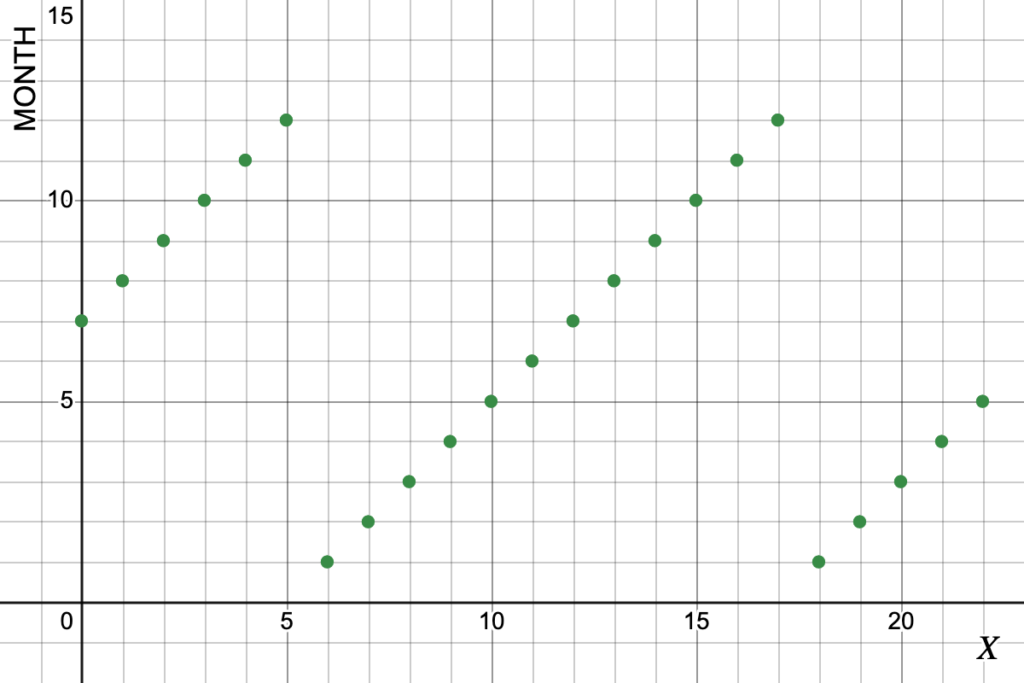
Another relevant function is a piecewise monotonic function. Consider the toMonth() function. This function, like many ClickHouse type conversion functions returning numbers or dates, is called piecewise monotonically increasing. At every point in its domain, toMonth() is monotonically increasing, but not on every interval; that is, there are “jumps” between the pieces where toMonth() is monotonically increasing. These jumps occur once the function has iterated through month 12 (December) and it starts over at 1 (January of the next year). The ranges where toMonth() is monotonically increasing (in between the jumps) are called the regions of monotonicity of toMonth() – in this case, the region of monotonicity is one year.
SELECT number AS x, toDate(addMonths(today(), x)) AS add1month, toMonth(add1month) AS month FROM numbers(23)This returns the following. As the variable add1month increases from one row to the next, month increases also.
┌──x─┬──add1month─┬───month─┐
│ 0 │ 2024-07-23 │ 7 │
│ 1 │ 2024-08-23 │ 8 │
│ 2 │ 2024-09-23 │ 9 │
│ 3 │ 2024-10-23 │ 10 │
│ 4 │ 2024-11-23 │ 11 │
│ 5 │ 2024-12-23 │ 12 │
│ 6 │ 2025-01-23 │ 1 │
│ 7 │ 2025-02-23 │ 2 │
│ 8 │ 2025-03-23 │ 3 │
│ 9 │ 2025-04-23 │ 4 │
│ 10 │ 2025-05-23 │ 5 │
│ 11 │ 2025-06-23 │ 6 │
│ 12 │ 2025-07-23 │ 7 │
│ 13 │ 2025-08-23 │ 8 │
│ 14 │ 2025-09-23 │ 9 │
│ 15 │ 2025-10-23 │ 10 │
│ 16 │ 2025-11-23 │ 11 │
│ 17 │ 2025-12-23 │ 12 │
│ 18 │ 2026-01-23 │ 1 │
│ 19 │ 2026-02-23 │ 2 │
│ 20 │ 2026-03-23 │ 3 │
│ 21 │ 2026-04-23 │ 4 │
│ 22 │ 2026-05-23 │ 5 │
└────┴────────────┴─────────┘
In general, a piecewise monotonically increasing function can look like this:

A monotonically decreasing function has corresponding terminology where the meaning is reversed. A monotonically decreasing function looks kind of like this:
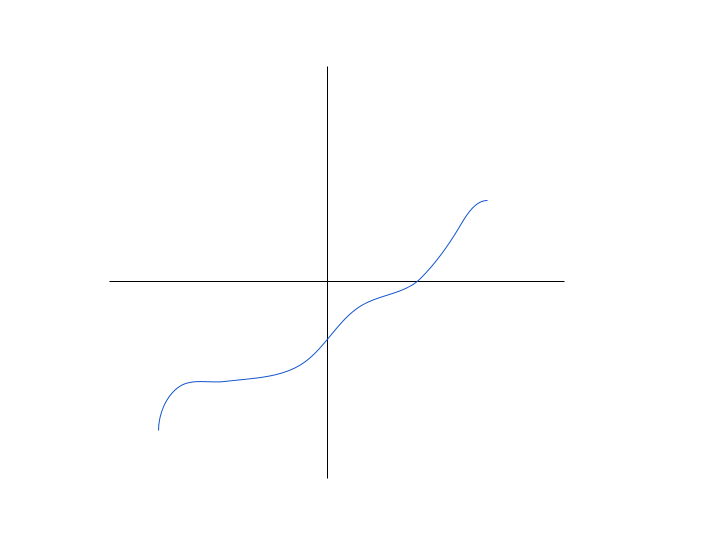
This next picture is a non-example. It is monotonically decreasing before x = 0 and monotonically increasing after, therefore it is neither monotonically decreasing nor monotonically increasing.
There are a few types of functions that will always be monotonically increasing as long as all their inputs are, so they preserve the monotonicity of their variables. Some single-variable monotonically increasing functions in ClickHouse are mathematical functions like sqrt(), factorial(), or exp(). Type conversion functions including toYear(), toMonth(), and toInt8() are (at least piecewise) monotonically increasing. Rounding functions like ceil(), round(), floor(), which can be single-variable or multivariable, are monotonically increasing functions, as are binary arithmetic functions like plus(), multiply(), and multiplyDecimal(). ClickHouse doesn’t check most multivariable functions for monotonicity, which is a limitation that we’ll discuss later in this article.
Investigating the first example
Let’s see what caused the difference in execution times in my initial example. Now, I will run six similar queries on the ontime_ref data set, each measuring over a different time period. The goal is to examine how ClickHouse’s monotonicity optimizations affect execution time of functions with varying levels of monotonicity. This gives some insight into how monotonicity checks work in ClickHouse. The queries have the following format, where x is some number that makes sense for the given time period:
SELECT count()
FROM default.ontime_ref
WHERE toTimePeriod(FlightDate) = xNote that within the same session, the SET min_bytes_to_use_direct_io = 1 command still applies, so I don’t have to run it separately for each query.
toYear()
SELECT count()
FROM default.ontime_ref
WHERE toYear(FlightDate) = 2015toDayOfYear()
SELECT count()
FROM default.ontime_ref
WHERE toDayOfYear(FlightDate) = 143toWeek()
SELECT count()
FROM default.ontime_ref
WHERE toWeek(FlightDate) = 21toMonth()
SELECT count()
FROM default.ontime_ref
WHERE toMonth(FlightDate) = 5toDayOfMonth()
SELECT count()
FROM default.ontime_ref
WHERE toDayOfMonth(FlightDate) = 23toDayOfWeek()
SELECT count()
FROM default.ontime_ref
WHERE toDayOfYear(FlightDate) = 6I ran each of these queries one more time with the additional command SETTINGS send_logs_level='trace' (note that this final execution is not included in the average execution time given below). The “trace” command gives a full explanation of all the steps that ClickHouse runs on its way to the final answer that it returns. Here is the interesting data that I got from the “trace” command for each test. I have ordered the functions below by the length of their region of monotonicity, descending, and then by the number of steps per region of monotonicity, descending.
| Function name | Region of monotonicity | Number of steps per region | Average execution time (milliseconds) | Marks read by primary key out of 24,415 | Rows processed out of 196.51 (millions) |
| toYear() | Everywhere | N/A | 78.4 | 1,308 | 10.49 |
| toDayOfYear() | Year | 365 | 107.4 | 1,183 | 9.59 |
| toWeek() | Year | 52-53 | 238.8 | 1,590 | 12.86 |
| toMonth() | Year | 12 | 135.6 | 3,180 | 25.65 |
| toDayOfMonth() | Month | 28-31 | 239.0 | 10,688 | 86.87 |
| toDayOfWeek() | Week | 7 | 355.6 | 23,169 | 187.70 |
And here is that same data:
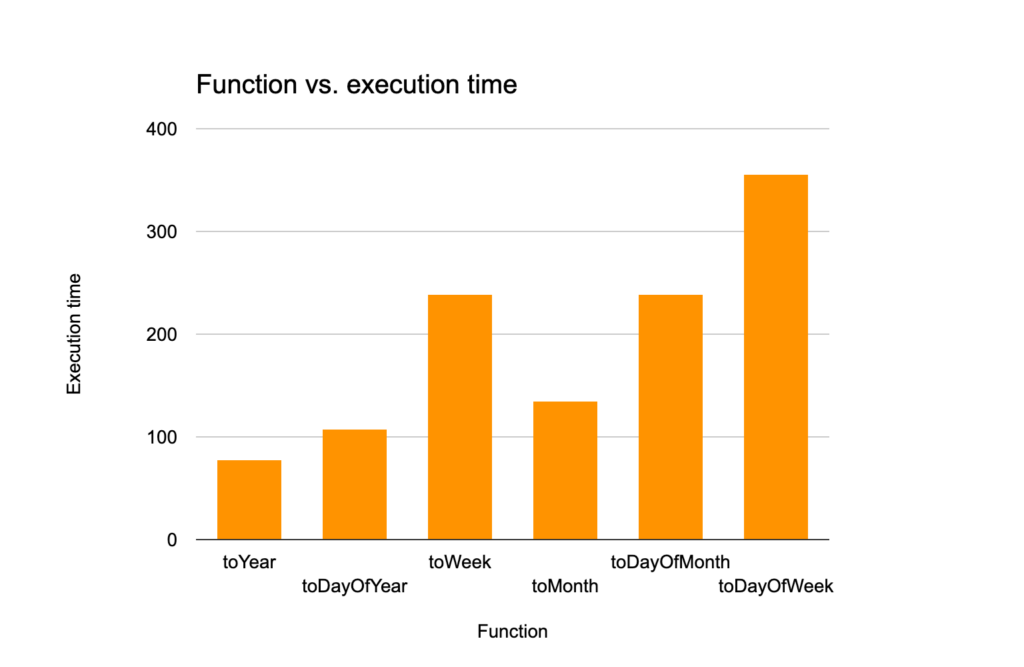
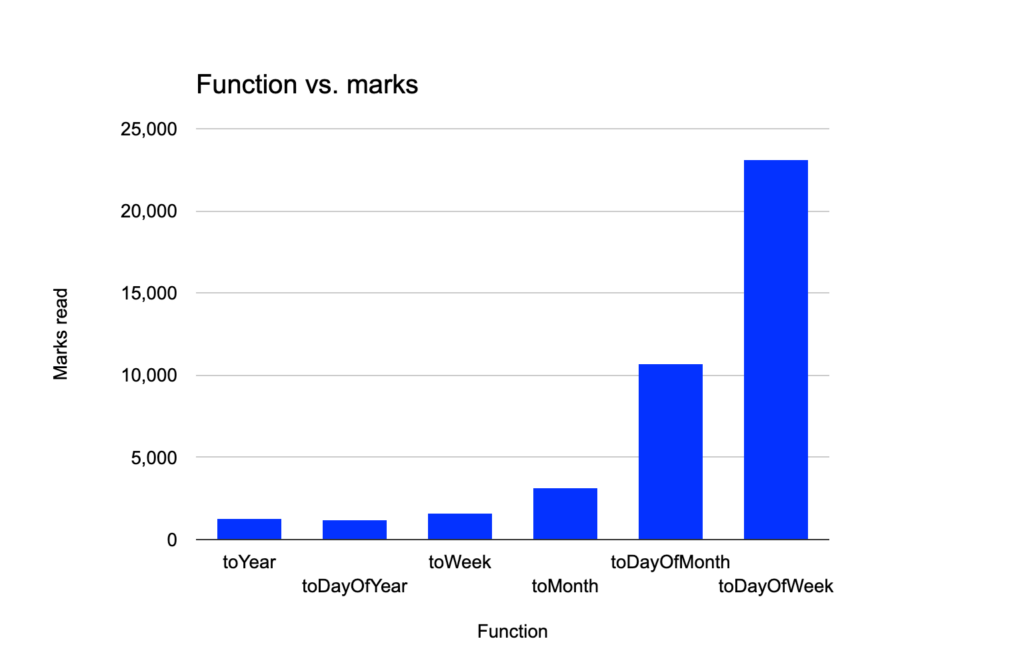
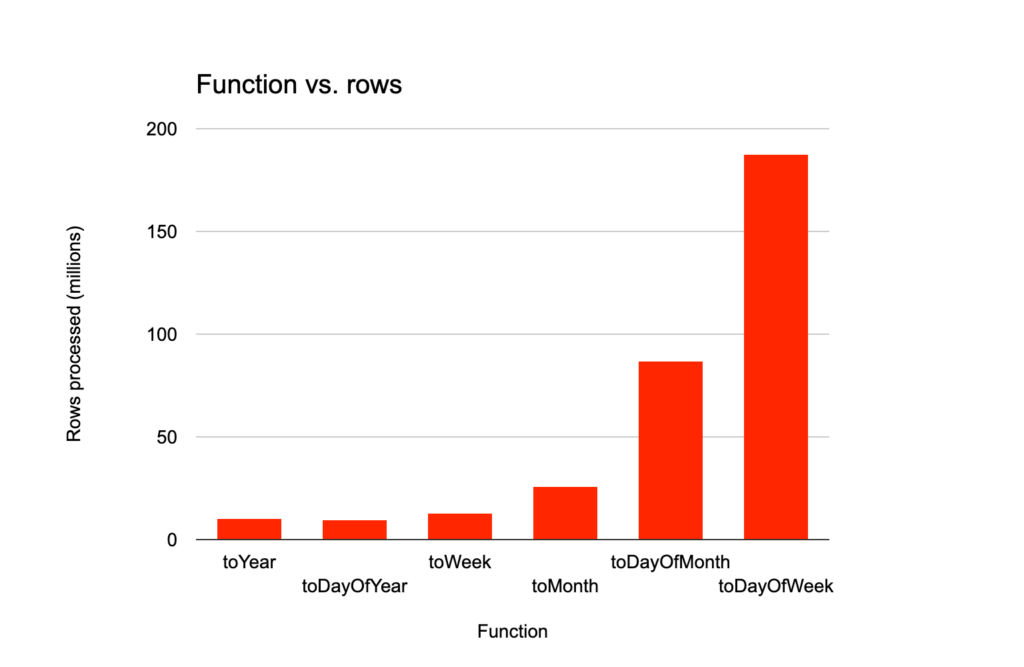
There is a neat pattern connecting the length of the region of monotonicity, the execution time, and the marks/rows read. As the length of the region and the steps per region increase, the execution time and marks/rows read all decrease. This must mean there is some optimization at play that takes advantage of the piecewise monotonicity of each of these functions. Let’s see how this optimization works.
How ClickHouse finds a monotonic function
For now, I’ll keep working with date/time transformations from one measure of time to another. Here is where the mathematical terminology diverges from ClickHouse code: ClickHouse doesn’t distinguish between completely monotonic or piecewise monotonic functions. Instead, it looks at a function on a given range, and asks if it is monotonic on that range. This is where the region of monotonicity is useful, because this is what determines where a piecewise monotonic function “looks” completely monotonic.
In the ClickHouse source code, the definition file (e.g. toYear.cpp) for every date/time transformation (T) includes the DateTimeTransforms.h file. Among other things, this file defines the factor transformation (FactorTransform in the code, but for now, call it F) for each T. For example, toDayOfWeek(), a piecewise monotonic function, is monotonically increasing on each week.
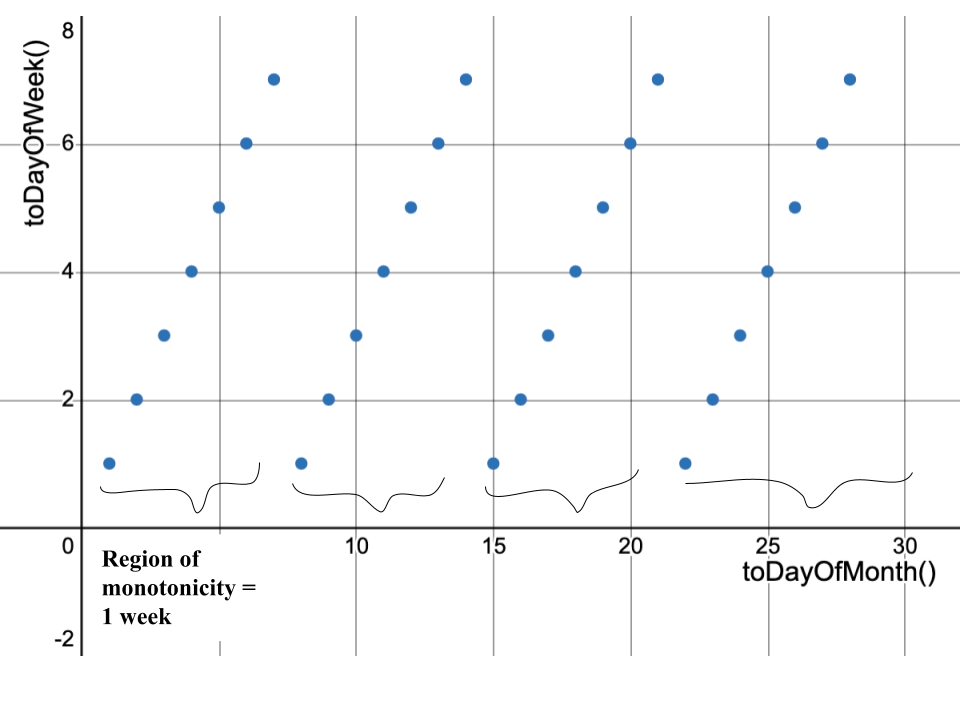
The code assigns F = toStartOfWeek for toDayOfWeek(). So for all x such that toStartOfWeek(x) = 2024-07-30, x is a date in the week of July 30th through August 4th, 2024, and toDayOfWeek() is monotonically increasing, with no jumps, over the range of such x. In other words, F defines the region of monotonicity of T. Notice that the regions where F is constant in the graph below are the same regions where toDayOfWeek() was monotonic on the previous graph.
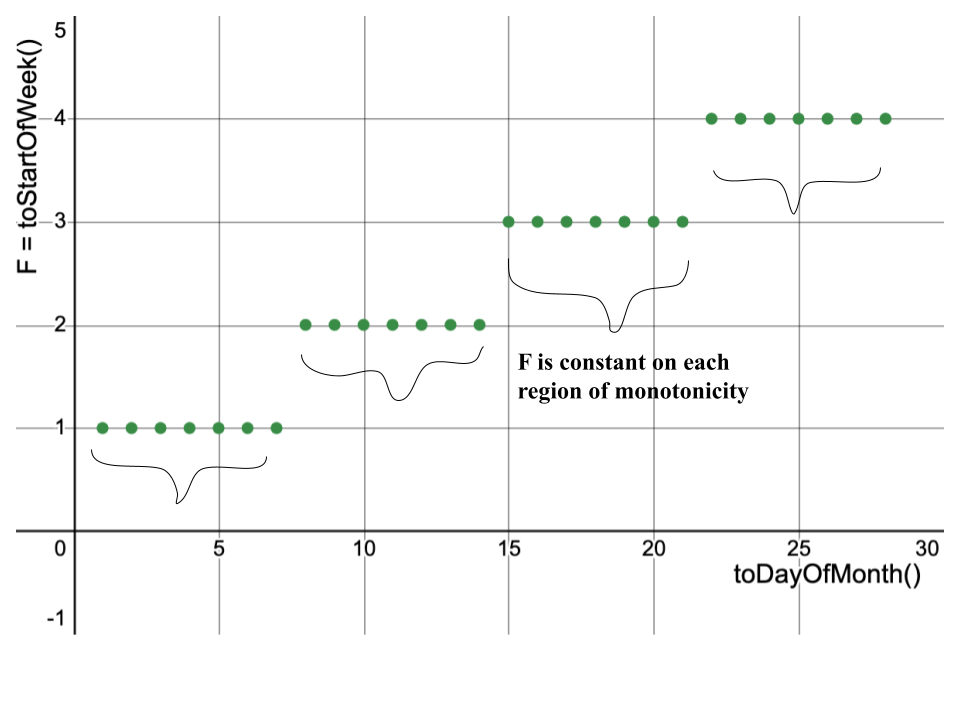
A function that is monotonically increasing everywhere, with an infinitely large region of monotonicity (such as toYear() or toStartOfWeek()) is assigned F = ZeroTransform.
Now that ClickHouse has the factor transformation F for each transformation T, the next step comes in the file IFunctionDateOrDateTime.h. Here, ClickHouse defines the method getMonotonicityForRange(IDataType,range) for each date/time transformation using F for a given T. If F = ZeroTransform, then ClickHouse marks T as monotonic everywhere. Otherwise, it checks that the value of F is the same for the left and right endpoints of the input range – looking at the previous graph, this step checks that the input range is a region where F is constant. If so, then the function is monotonic on the range, and ClickHouse determines whether it is monotonically increasing or decreasing. I’ve summarized this in the diagram below:
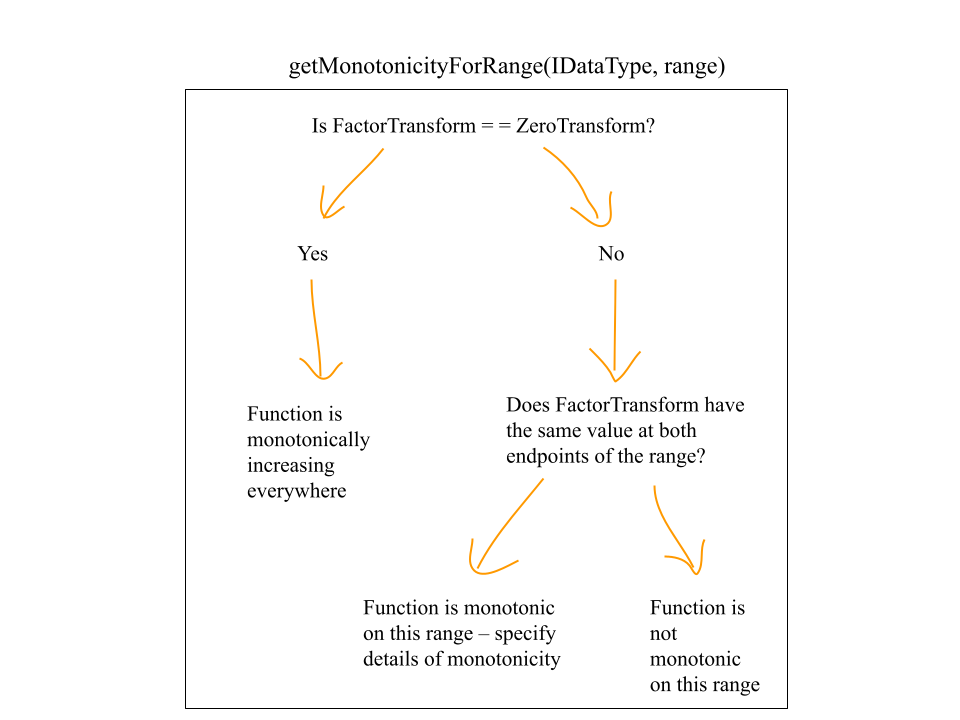
By default, a function in ClickHouse is not marked as monotonic. All date/time transformations are (at least piecewise) monotonically increasing, therefore it’s worth dedicating lots of code to finding their regions of monotonicity.
What does ClickHouse do when it knows a function is monotonic?
The ontime_ref table has a primary key index organized by Carrier, FlightDate and partitioned by year. During a range query, this index allows ClickHouse to skip over unnecessary rows. Here’s how the primary key index works on a range query without a function vs. a range query with a monotonic function.
Example 1: no function
This query returns flights from the month of May 2015 by using a range for FlightDate.
SELECT count()
FROM default.ontime_ref
WHERE FlightDate BETWEEN '2015-05-01' AND '2015-05-31'Suppose the following table is a section of the primary key index. (These aren’t the exact values for granules in the index but show the idea.) Each granule is labeled with the minimum-value pair of Carrier, FlightDate occurring in that granule. Since the ontime_ref table is ordered by Carrier, FlightDate in ascending order, the minimum entry is the first in that granule. I’ve highlighted in green the granules that ClickHouse can read to find flights satisfying the above query.
| Granule | Carrier | FlightDate |
| 0 | ‘AA’ | ‘2015-01-01’ |
| 1 | ‘AA’ | ‘2015-06-10’ |
| 2 | ‘AA’ | ‘2015-12-21’ |
| 3 | ‘AS’ | ‘2015-03-15’ |
| 4 | ‘AS’ | ‘2015-08-11’ |
| 5 | ‘AS’ | ‘2015-11-12’ |
| 6 | ‘DL’ | ‘2015-01-13’ |
| 7 | ‘DL’ | ‘2015-05-09’ |
| 8 | ‘DL’ | ‘2015-09-18’ |
| 9 | ‘DL’ | ‘2015-12-25’ |
ClickHouse has to read granule 0 because it knows that some of the entries with the relevant FlightDate can be found between ‘2015-01-01’ and ‘2015-06-10’. Later, it reads both granules 6 and 7 because the month of May 2015 spans both of these granules.
Example 2: piecewise monotonic function
When considering this section of the primary key index that is all from 2015, the next example is virtually the same as the last one. However, ClickHouse treats this query slightly differently because of the toMonth() function in the WHERE clause.
SELECT count()
FROM default.ontime_ref
WHERE toMonth(FlightDate) = 5| Granule | Carrier | FlightDate | toMonth() |
| 0 | ‘AA’ | ‘2015-01-01’ | 1 |
| 1 | ‘AA’ | ‘2015-06-10’ | 6 |
| 2 | ‘AA’ | ‘2015-12-21’ | 12 |
| 3 | ‘AS’ | ‘2015-03-15’ | 3 |
| 4 | ‘AS’ | ‘2015-08-11’ | 8 |
| 5 | ‘AS’ | ‘2015-11-12’ | 11 |
| 6 | ‘DL’ | ‘2015-01-13’ | 1 |
| 7 | ‘DL’ | ‘2015-05-09’ | 5 |
| 8 | ‘DL’ | ‘2015-09-18’ | 9 |
| 9 | ‘DL’ | ‘2015-12-25’ | 12 |
Now, ClickHouse reads all the same granules as in the previous example. It also needs to read granules 2 and 5 because toMonth() is not monotonically increasing (think: order-preserving) between granules 2 – 3 and 5 – 6. Therefore, ClickHouse can no longer make assumptions about where the month of May is located, as it did previously, and it reads the granules spanning this gap in monotonicity. Queries containing toWeek() and toDayOfWeek(), which have more gaps in monotonicity than toMonth(), would force ClickHouse to read even more rows.
However, when ClickHouse encounters a non-monotonic function like toString(FlightDate), it can make no assumptions about the order of the outputs and it has to read all rows of the table. This explains the difference in execution time in the very first example I showed, comparing toYear(), toWeek(), and toString() queries: a monotonic function reads fewer rows than a piecewise monotonic function, and a non-monotonic function reads the most.
Finding multivariable monotonically increasing functions in ClickHouse
You can check the monotonicity of a single-variable function by increasing the input and seeing if it consistently increases or decreases. It’s much harder to prove monotonicity definitively for multivariable functions, because changing different variables can have different effects on the function output. The only multivariable functions (that I know of) that are marked as monotonic in ClickHouse are, for a constant a or b, divide(a,b), intDiv(a,b), minus(a,b), and plus(a,b); all other multivariable functions default to “non-monotonic” in ClickHouse, even when they really are monotonic. As a result, the optimization I described above doesn’t extend to most multivariable functions, which leaves a clear gap between what is possible and what has been implemented. Barring more complex code, one way to bridge this gap is with tests that may prove if a function is monotonic on a range, but that don’t work for all monotonic functions. While researching monotonicity in ClickHouse, I thought of a few such tests that could check monotonicity for certain multivariable functions in ClickHouse. If implemented correctly, ClickHouse could label certain multivariable functions as monotonic and run faster.
plus(a,b) and multiply(a,b)
In the file FunctionBinaryArithmetic.h, plus(a,b) is checked for monotonicity only when a is constant and b is a variable, or vice versa. multiply(a,b) isn’t checked for monotonicity at all here. But it would be simple to extend this to two non-constant variables. plus() preserves the increasing monotonicity of its variables, a fact I can quickly prove:
Let ![]() ≤
≤ ![]() and
and ![]() ≤
≤ ![]() – the a-variables and b-variables are both monotonically increasing. Then
– the a-variables and b-variables are both monotonically increasing. Then ![]() +
+ ![]() ≤
≤ ![]() +
+ ![]() ≤
≤ ![]() +
+ ![]() . Therefore
. Therefore ![]() +
+ ![]() ≤
≤ ![]() +
+ ![]() , so
, so plus() is monotonically increasing.
Similarly, multiply() preserves the increasing monotonicity of its variables:
Let 0 ≤ ![]() ≤
≤ ![]() and 0 ≤
and 0 ≤ ![]() ≤
≤ ![]() – again, the a-variables and b-variables are both monotonically increasing. Then
– again, the a-variables and b-variables are both monotonically increasing. Then ![]() ≤
≤ ![]() ≤
≤ ![]() . Therefore
. Therefore ![]() ≤
≤ ![]() , so
, so multiply() is monotonically increasing for non-zero variables – in the case of ClickHouse, this means unsigned integers.
By switching ![]() with
with ![]() and
and ![]() with
with ![]() in both of these proofs, we can also conclude that
in both of these proofs, we can also conclude that plus(a,b) and multiply(a,b) are monotonically decreasing when both a and b are. You can think of this as “reversing time”, or flipping a monotonically increasing graph across the vertical axis, which results in a monotonically decreasing graph.
As defined in FunctionBinaryArithmetic.h, getMonotonicityForRange(IDataType, range) returns a vector of four boolean values for plus(a,b). For now, the first two booleans in this vector, is_monotonic and is_positive_monotonicity, are needed. is_positive_monotonicity is true when the function is monotonically increasing and false when it is monotonically decreasing.
Well, say we have plus(a,b) and multiply(a,b) where a and b are both non-constant variables. A simple way to check if either of these functions is monotonic on a given range is by using information about plus(a,0) and plus(0,b). If plus(a,0)->getMonotonicityForRange(IDataType,range) and plus(0,b)->getMonotonicityForRange(IDataType,range) both return vectors containing is_monotonic == true and is_positive_monotonicity == true, then both functions are monotonically increasing. This is because a + 0 is monotonically increasing if and only if a is monotonically increasing. Therefore the variables a and b are both monotonically increasing, and since plus(a,b) and multiply(a,b) both preserve increasing monotonicity of variables, plus(a,b) and multiply(a,b) are monotonically increasing as well. This outcome occurs for multiply(a,b) only when a and b are unsigned integers.
Conversely, if plus(a,0)->getMonotonicityForRange(IDataType,range) and plus(0,b)->getMonotonicityForRange(IDataType,range) both return vectors containing is_monotonic == true and is_positive_monotonicity == false, then both functions are monotonically decreasing. Therefore the variables a and b are both monotonically decreasing, and since plus(a,b) and multiply(a,b) preserve the decreasing monotonicity of variables, plus(a,b) and multiply(a,b) are monotonically decreasing as well (again, multiply(a,b) needs a and b to be unsigned integers for this to be true).
Visually, this is:

This is not a conclusive test; either of these functions may be monotonically increasing even if plus(a,0) and plus(0,b) are not. This test may tell the user if plus(a,b) is monotonically increasing, but the absence of a result doesn’t mean it’s not monotonically increasing, and likewise for multiply(a,b).
This method for checking monotonicity also works for adding and multiplying functions with different data types, e.g. addDays(date,num). A general algorithm that can be applied to other multivariable functions in ClickHouse is: if a function preserves variable monotonicity, use the appropriate single-variable monotonically increasing functions to check if all input variables are monotonic in the same direction. If so, then you can conclude that the multivariable function is also monotonic in that direction.
Conclusion
Monotonic functions are a major optimization in ClickHouse that are worth understanding and leveraging in your queries. The mathematical principles of function behavior, while seemingly abstract, provide tangible benefits by enabling efficient data skipping and faster query processing. This article showed practical examples of how monotonicity affects I/O and query response time. You might already have had at least one “aha!” feeling about why ClickHouse performs so quickly. By continuing to explore and extend these optimizations to multivariable functions, ClickHouse users can push the boundaries of modern data analysis with centuries-old mathematical knowledge.
Acknowledgements
Thank you to Alsu Giliazova, Arthur Passos, Alexander Zaitsev, Vasily Nemkov, and Robert Hodges for your help with researching and writing this article.
ClickHouse® is a registered trademark of ClickHouse, Inc.; Altinity is not affiliated with or associated with ClickHouse, Inc.
